Autor
Zigurat Global Institute of Technology
Categorias
 Si a todo esto le añadimos el hecho de que realmente la “Las estructuras se comportan como se construyen, no como se modelan" frase archiconocida del ingeniero Eduardo Torroja nos obliga a que dentro del proceso global de diseño y cálculo estructural deben tenerse en cuenta ambas concepciones de forma simultánea, tanto las relativas a las conexiones como las relativas a las barras.
La estructura metálica no es una excepción.
En este artículo nos centramos en el diseño de la conexión soldada que debe ser capaz de transmitir esfuerzos de corte y torsión. Para el desarrollo del ejemplo práctico nos apoyamos en una hoja de cálculo MathCad donde implementamos todo el procedimiento.
Si a todo esto le añadimos el hecho de que realmente la “Las estructuras se comportan como se construyen, no como se modelan" frase archiconocida del ingeniero Eduardo Torroja nos obliga a que dentro del proceso global de diseño y cálculo estructural deben tenerse en cuenta ambas concepciones de forma simultánea, tanto las relativas a las conexiones como las relativas a las barras.
La estructura metálica no es una excepción.
En este artículo nos centramos en el diseño de la conexión soldada que debe ser capaz de transmitir esfuerzos de corte y torsión. Para el desarrollo del ejemplo práctico nos apoyamos en una hoja de cálculo MathCad donde implementamos todo el procedimiento.
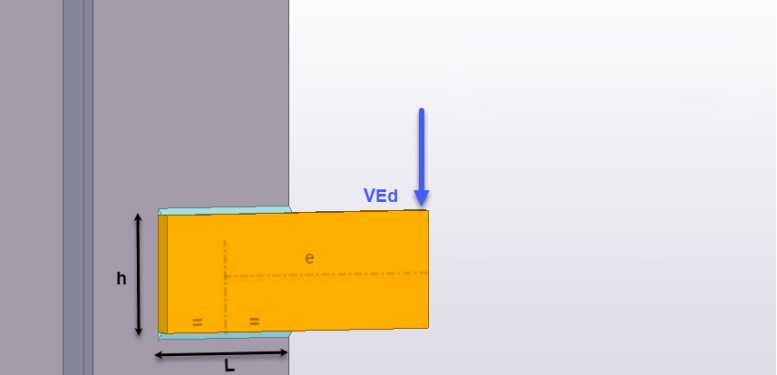
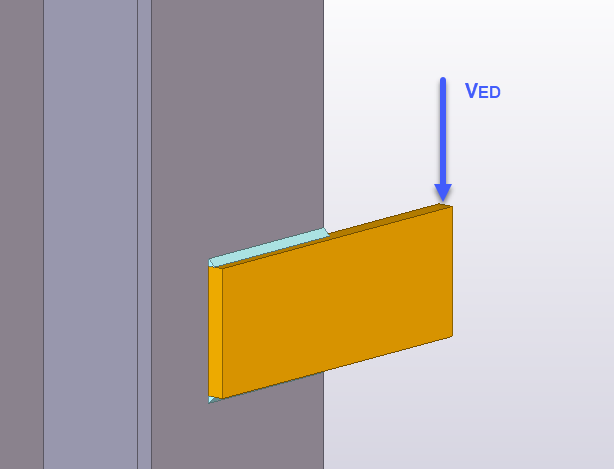 En este caso se trata de una unión que consiste en una placa – ménsula soldada a otro elemento metálico bien podría ser una columna.
Se disponen dos cordones de soldadura laterales en ángulo. Como se puede observar la conexión está solicitada por un caga vertical “VEd” excéntrica respecto al cdg de la distribución de las soldaduras.
En este caso se trata de una unión que consiste en una placa – ménsula soldada a otro elemento metálico bien podría ser una columna.
Se disponen dos cordones de soldadura laterales en ángulo. Como se puede observar la conexión está solicitada por un caga vertical “VEd” excéntrica respecto al cdg de la distribución de las soldaduras.
 Arrancaremos mirando la conexión frontalmente y analizando qué esfuerzos existen en el plano abatido frontal:
Arrancaremos mirando la conexión frontalmente y analizando qué esfuerzos existen en el plano abatido frontal:
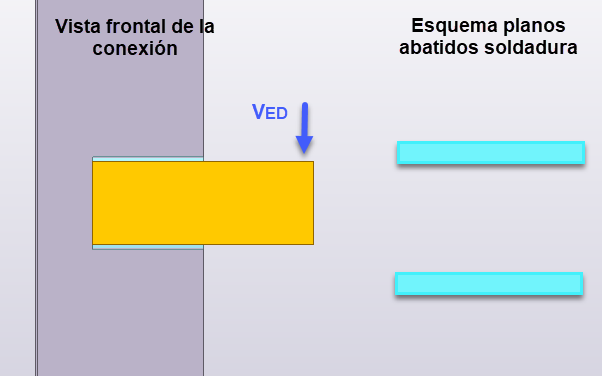 Vemos como la excentricidad en el esfuerzo aplicado “e” provoca que la conexión deba ser capaz de transmitir un esfuerzo de corte “VED” y, adicionalmente, un momento torsor “MT = VEd · e”.
Vemos como la excentricidad en el esfuerzo aplicado “e” provoca que la conexión deba ser capaz de transmitir un esfuerzo de corte “VED” y, adicionalmente, un momento torsor “MT = VEd · e”.
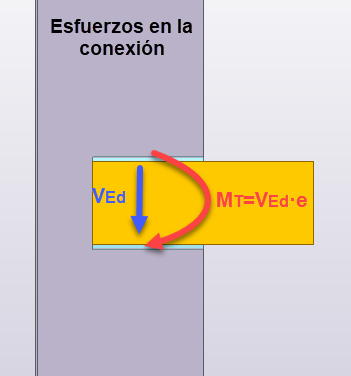 El Método de las dos fuerzas permite descomponer el efecto del momento torsor “MT” en un par de fuerzas. El criterio de validez para poder aplicar el método es el siguiente:
El Método de las dos fuerzas permite descomponer el efecto del momento torsor “MT” en un par de fuerzas. El criterio de validez para poder aplicar el método es el siguiente:
 Una vez validado el método arrancamos descomponiendo el “MT= VEd · e” en un par de fuerzas “T” que solicitan a los dos cordones.
A su vez el esfuerzo cortante “VED” solicita a ambos cordones por igual:
Lo vemos:
Una vez validado el método arrancamos descomponiendo el “MT= VEd · e” en un par de fuerzas “T” que solicitan a los dos cordones.
A su vez el esfuerzo cortante “VED” solicita a ambos cordones por igual:
Lo vemos:
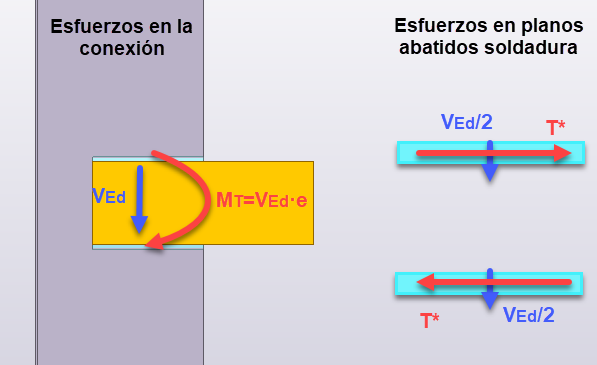 En este caso particular ambos cordones se encuentran solicitados de igual forma y con valores idénticos.
Introduciendo valores a nuestro problema…
En este caso particular ambos cordones se encuentran solicitados de igual forma y con valores idénticos.
Introduciendo valores a nuestro problema…
 …. tenemos los esfuerzos sobre los planos abatidos de los cordones siguientes:
…. tenemos los esfuerzos sobre los planos abatidos de los cordones siguientes:

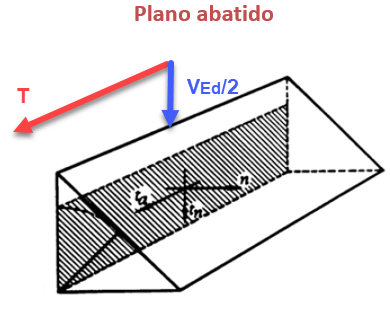 Y lo cuantificamos:
Y lo cuantificamos:
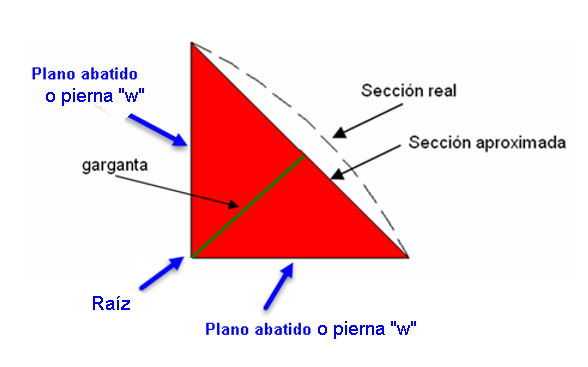
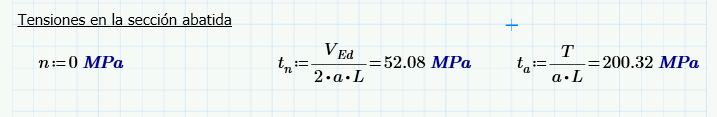 Llegados hasta aquí solo nos queda evaluar las tensiones que se producen en el plano de garganta o plano resistente de la soldadura.
Para esta conversión de esfuerzos-tensiones en el plano abatido a esfuerzos-tensiones en el plano de garganta tenemos las siguientes expresiones (considerando que el plano de garganta se encuentra a 45º):
Llegados hasta aquí solo nos queda evaluar las tensiones que se producen en el plano de garganta o plano resistente de la soldadura.
Para esta conversión de esfuerzos-tensiones en el plano abatido a esfuerzos-tensiones en el plano de garganta tenemos las siguientes expresiones (considerando que el plano de garganta se encuentra a 45º):
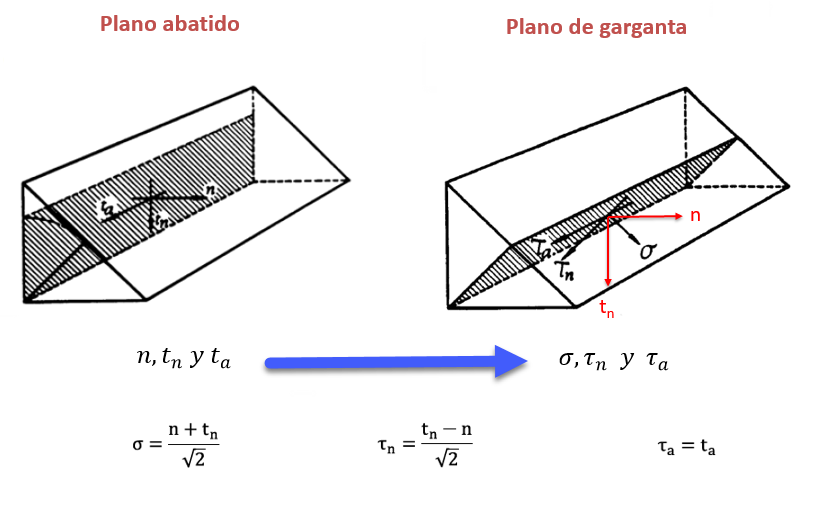 Para el ejemplo que estamos resolviendo tenemos:
Para el ejemplo que estamos resolviendo tenemos:
 Como estamos viendo estamos desgranando las tensiones en el cordón de soldadura según la dirección de los esfuerzos aplicados. Con esto hemos sido capaces de obtener las tensiones “ ” que debe ser capaz de resistir el plano de garganta o plano resistente. Esta manera de proceder forma parte del “Método direccional” recogido en numerosas normativas de cálculo estructural en acero como el EC 3.
Seguidamente compondremos por Von Mises las tensiones actuantes en el plano de garganta obteniendo la tensión de comparación correspondiente “ ”
Luego por último compararemos la tensión de comparación “ ” con la resistencia del cordón a fin de valorar si el ancho de garanta “a” es suficiente o si por el contrario debemos aumentarlo.
Par la primera comprobación tenemos:
Como estamos viendo estamos desgranando las tensiones en el cordón de soldadura según la dirección de los esfuerzos aplicados. Con esto hemos sido capaces de obtener las tensiones “ ” que debe ser capaz de resistir el plano de garganta o plano resistente. Esta manera de proceder forma parte del “Método direccional” recogido en numerosas normativas de cálculo estructural en acero como el EC 3.
Seguidamente compondremos por Von Mises las tensiones actuantes en el plano de garganta obteniendo la tensión de comparación correspondiente “ ”
Luego por último compararemos la tensión de comparación “ ” con la resistencia del cordón a fin de valorar si el ancho de garanta “a” es suficiente o si por el contrario debemos aumentarlo.
Par la primera comprobación tenemos:
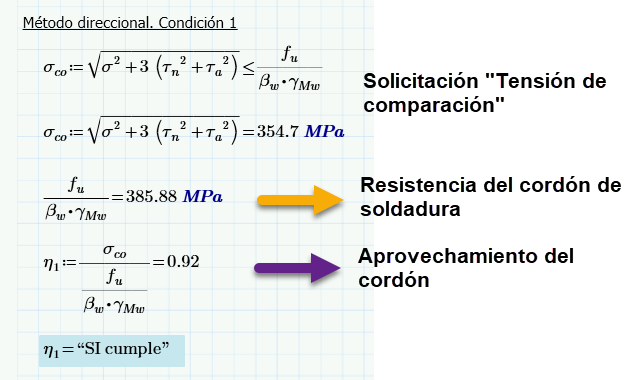 Finalmente también se requiere que las tensiones normales “σ” exclusivamente no superen la resistencia del cordón sin afectarla por el coeficiente de correlación “βw”:
Finalmente también se requiere que las tensiones normales “σ” exclusivamente no superen la resistencia del cordón sin afectarla por el coeficiente de correlación “βw”:
 Como vemos el ancho de garganta a=6mm es suficiente para hacer frente a la solicitación. Se requiere una longitud del cordón L=150mm y ambos cordones se encuentran trabajando al 92% de su capacidad.
Todo este contenido y mucho más, forma parte del Máster Internacional de Estructuras Metálicas y Mixtas en Edificación de ZIGURAT……
Como vemos el ancho de garganta a=6mm es suficiente para hacer frente a la solicitación. Se requiere una longitud del cordón L=150mm y ambos cordones se encuentran trabajando al 92% de su capacidad.
Todo este contenido y mucho más, forma parte del Máster Internacional de Estructuras Metálicas y Mixtas en Edificación de ZIGURAT……

Zigurat Global Institute of Technology