En este artículo se expone lo básico del beneficioso efecto que puede darse en una viga donde se desarrolle un cierto efecto membrana.
Por efecto de la carga vertical, incluso por peso propio, y a menos que en los apoyos exista posibilidad de coacción horizontal el hecho de que la pieza no cambia de longitud implica un pequeño corrimiento hacia el centro ∆l.
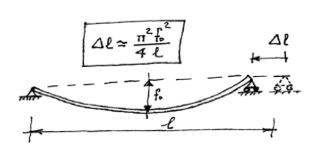Ante todo hay que recordar un par de conceptos de Teoría de Estabilidad de Estructuras muy elementales:
- Una viga cargada transversalmente experimenta un aumento de flecha sobre la que le corresponde a la carga si simultáneamente está sometida a un axil de compresión H.
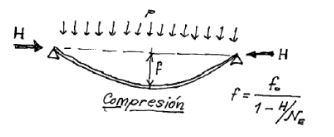Es decir que si la carga transversal es p, en la viga biapoyada (un apoyo fijo y el otro deslizante) de inercia I y de luz l , por flexión se produce :
f0 = 5/384 pl4/E I
Al darse un axil de compresión de valor H se experimenta una amplificación:
1/ 1- H/NE
Siendo NE la carga crítica de Euler en el plano de la flexión.
NE = π2 E I / l2.
En el caso de que sea el axil H de tracción se da una disminución, el factor es entonces:
La reducción de flecha es : 1/ 1 + H/NE
2. Cuando los dos apoyos están fijados, es decir cuando pueden soportar reacciones horizontales, se puede demostrar que al impedirse el corrimiento indicado aparece una reacción que justamente compensa ese estiramiento por acción de axil
∆M = H l / E A
Igualando esos corrimientos y operando se llega a una expresión sencilla, a resolver por tanteos, que permite calcular esa reacción H, en función del parámetro α = H/NE
α(1+α)2 = A f02/ 4 I
Esto supone muchas ventajas en el proyecto de escotillas, tapas, pavimentos de chapa e incluso comportamiento dinámico de escalones y resistencia a fuego/explosiones de correas de cubierta.
Lo esencial es que los extremos resistan más que esa posible fuerza H que se crea al impedirse el corrimiento horizontal.
Ejemplo (efecto membrana)
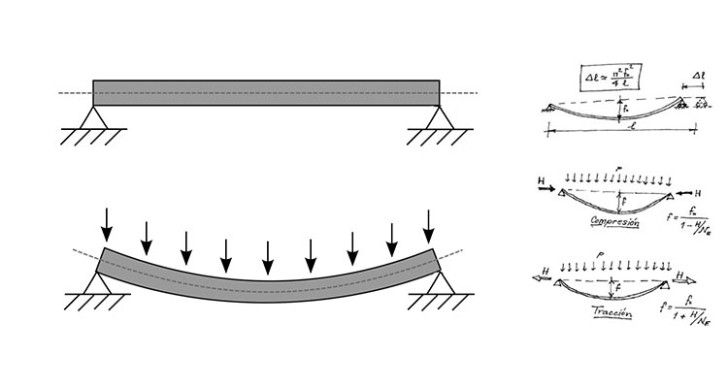
Planteamiento convencional.
Sea un pavimento o piso de chapa de acero S275 ,de t= 12 mm de espesor apoyada entre crujías en vanos regulares de una luz de 1500 mm.
La carga de diseño es de 2400 kgf/m2 ≈ 24 kN/m2, que puede corresponder a un sobrecarga viva de acopio, ya factorizada, o a una sobrepresión accidental.
Incluso como viga continua, en su vano extremo tendría una flecha en mitad del vano:
f= pl4/ 158 E I = 25 mm
y un flector en apoyo M= 0.107 pl2 = 5778 mm N/mm
La tensión en la chapa se eleva a s = 6M/t2 = 240 N/mm2. Es decir del orden de un 90% del límite elástico.
Opción membrana:
Si se recurre a soldar apoyos (ranura o tapón) y aplicar la teoría de membrana se puede bajar el espesor de forma considerable para ese mismo nivel tensional.
Efectivamente con t=8mm, ahora se tiene en una franja unitaria I= 42.66 mm4
y A=8mm, siendo la carga critica de Euler NE= 39.29 N.
La flecha isostática ahora con apoyos biarticulados es:
f0= ( 5/384) pl4/ E I = 176.5 mm
El flector isostático M0 = pl2/8 = 6750 mm N/mm
El parámetro a debe satisfacer:
a(1+a)2 = A f02/ 4 I = 8 176.52 / 4 42.66 = 1460
Procediendo por tanteos se obtiene a= 10.69
Por lo tanto la flecha real vale f= f0 /( 1+a) = 176.5 /(1+10.69) = 15 mm.
Es bastante inferior a la de la chapa anterior.
La reacción horizontal en apoyos H = a NE = 10.69 39.29 = 420 N
El flector real vale:
M= M0 – H f = 6750 – 420 15 = 450 mm N/mm
Ahora hay que sumar la tensión de flexión y la tensión de membrana
s = 6M/t2 + H /t = 6 450 / 82 + 420 / 8 = 42 + 53 = 95 N/mm2
Conclusión efecto membrana:
Adviértase que con una reducción de peso del 33% el nivel tensional resulta del orden del 33 % del límite elástico. Se ahorra material y se gana en resistencia.
En placas con sus cuatro bordes soldados este efecto es todavía más ventajoso. Es recomendable utilizar las tablas de la parte 1.7 de Eurocódigo 3.
