Esenciales del diseño paramétrico y algorítmico para impulsar la creatividad en la construcción

El uso de herramientas computacionales en oficinas de diseño es común desde mediados de los años 90 (VOLTOLINI, 2016). Estas herramientas de Diseño Asistido por Computadora (CAD) han optimizado significativamente la producción de proyectos, especialmente en términos de representación gráfica y visualización.

Los procesos de diseño son amplios y no universales, ya que cada individuo tiene procesos intrínsecos para expresar ideas. Sin embargo, se observan procesos comunes cuando se utilizan tecnologías específicas. Con las herramientas tradicionales (CAD), un proceso aditivo de inserción de información, la comprensión y generación resultan de la forma o composición espacial, conocido como FormMaking. En contraste, nuevas metodologías como el Diseño Paramétrico y la Modelación Algorítmica se inclinan más hacia FormFinding, un proceso que busca la forma basada en parámetros, ya sean fijos o manipulables (CARDOSO, 2017).

A través de métodos de Diseño Generativo (DG), los Algoritmos Evolutivos (AE) se han empleado en proyectos arquitectónicos, ayudando a dar forma tanto a la estructura de un edificio como a disposiciones geométricas que se alinean con factores ambientales. La idea fundamental es inspirarse en teorías evolutivas de la naturaleza para generar nuevas soluciones de manera más rápida.

Los algoritmos evolutivos se han utilizado para diseñar diversas tipologías de productos, desde aviones hasta chips de computadora, siendo adecuados para problemas donde la solución deseada no se conoce de antemano y el espacio de búsqueda es vasto y complejo.

En este enfoque de diseño, los algoritmos evolutivos simulan el proceso de selección natural, donde los miembros más aptos de una población se seleccionan para reproducirse y pasar sus características a la siguiente generación, generando múltiples soluciones (poblaciones). El algoritmo comienza con una población de diseños aleatorios, evaluando cada uno contra el objetivo deseado. Las soluciones se evalúan en relación con un conjunto de criterios llamados funciones de aptitud (ROHRMANN, 2019).

Los diseños más aptos se eligen para la reproducción, y sus características se combinan para crear nuevos diseños. Las soluciones que demuestran buen rendimiento según las funciones de aptitud se seleccionan para formar una nueva generación de soluciones. Este proceso se repite hasta alcanzar el objetivo deseado o la mejor opción dentro de un proceso finito (VOLTOLINI, 2020). La principal ventaja de este enfoque es su capacidad para encontrar excelentes soluciones para problemas difíciles de resolver para los humanos.

La Historia de los Algoritmos Evolutivos: Un Nuevo Paradigma de Diseño

La historia de la programación de algoritmos evolutivos comienza con la idea de usar la evolución como metáfora para resolver problemas. Darwin, en su libro "El Origen de las Especies," propuso que los organismos evolucionan mediante un proceso de selección natural, donde los individuos más aptos tienen más probabilidades de sobrevivir y reproducirse. Esta lógica puede aplicarse a la resolución de problemas usando una población de soluciones potenciales, seleccionando las más aptas. Los primeros trabajos relacionados con la computación evolutiva se publicaron a mediados de los años 50 (JONG et al., 1997). Destacan los trabajos de Friedberg (1958), Friedberg et al. (1959) y Fraser (1957). En el mismo periodo, precisamente en 1962, Bremermann presentó sus primeros intentos de aplicar la simulación evolutiva y la optimización numérica para resolver problemas, desarrollando algunas de las primeras teorías sobre Algoritmos Evolutivos (JONG et al., 1997).

A mediados de los años 60, se establecieron las tres formas principales de Algoritmos Evolutivos (AE): la Programación Evolutiva (EP) por Lawrence Fogel en San Diego, California; los Algoritmos Genéticos (GA) por Holland de la Universidad de Michigan; y las Estrategias Evolutivas (ES) desarrolladas por un grupo de estudiantes en Berlín: Nienert, Rechenberg y Schwefel (JONG et al., 1997). Estas tres técnicas de algoritmos evolutivos se conocen colectivamente como Algoritmos Evolutivos (AEs) (COELLO et al., 2007).

En los años 90, tuvo lugar el International Workshop on Parallel Problem Solving from Nature en Dortmund, fomentando la interacción entre diversas comunidades de investigación de algoritmos evolutivos. La interacción constante y creciente llevó a la terminología conocida como Computación Evolutiva, aún utilizada hoy en día (SCHWEFEL y MÄNNER, 1991). Los Algoritmos Evolutivos se han empleado para diseñar y optimizar una amplia gama de productos en diferentes sectores, incluidos proyectos arquitectónicos. En las últimas décadas, una de las áreas principales de exploración en arquitectura es el uso de herramientas computacionales aplicadas al proceso de diseño (KESTELIER y PETERS, 2006).

Algunas Definiciones Clave

Para una mejor comprensión, presentaremos definiciones de conceptos relacionados con los Algoritmos Evolutivos, como Algoritmo, Modelación Algorítmica, Programación Visual, Diseño Paramétrico, Modelo Paramétrico y Diseño Generativo.

Algoritmos: Los Pilares del Diseño Innovador

En su reconocido libro "Algorithmic Architecture," Terzidis define un Algoritmo como (TERZIDIS, 2013): "Un algoritmo es un procedimiento computacional para resolver un problema en un número finito de pasos. Involucra deducción, inducción, abstracción, generalización y lógica estructurada. Es la extracción sistemática de principios lógicos y el desarrollo de un plan de solución genérico" (TERZIDIS, 2006, p. 159).

Modelación Algorítmica: Más Allá de los Límites Tradicionales

Se refiere específicamente al uso de lenguajes de script que permiten a los diseñadores ir más allá de las limitaciones de las interfaces de software de diseño convencional, ampliando la capacidad de modelar mediante la manipulación directa no de la forma sino del código. La modelación algorítmica generalmente puede realizarse utilizando lenguajes de programación de computadoras como RhinoScript. Sin embargo, con la dificultad de la programación, aplicaciones como Generative Components y Grasshopper permiten el uso de código con formas pictóricas (componentes) para la automatización (LEACH, 2014).

Programación Visual: Creando el Futuro del Diseño con Arrastrar y Soltar

La programación visual permite la creación de algoritmos mediante la manipulación de componentes gráficos como íconos, botones y símbolos. Es posible realizar modelación paramétrica con características de programación visual sin necesidad de escribir una línea de código de texto. A diferencia del código tradicional donde se escriben líneas de texto en un compilador, la programación visual utiliza programas que contienen una interfaz donde se introducen componentes para formar el código que realizará la tarea. Un ejemplo de tal programa es Grasshopper, un complemento para Rhinoceros (CELANI y VAZ, 2012).

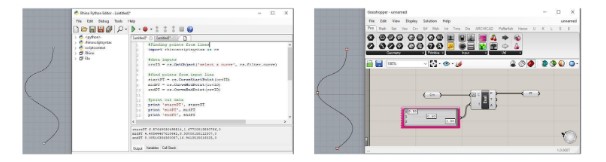
Figure 1: Textual Programming vs. Visual Programming – Start, Mid, End point of a curve.Source: The author.

Diseño Paramétrico: Un Cambio Radical en la Evolución Dinámica de Proyectos

El software paramétrico utiliza parámetros numéricos y geométricos, permitiendo ajustes incrementales a un elemento que consecuentemente afecta todo el modelo en una reacción en cadena. A diferencia del proceso tradicional, el diseño paramétrico interconecta partes del proyecto y las altera juntas, de manera integrada. Esta conexión permite cambios, relaciones, adiciones y reparaciones en el diseño, reduciendo el retrabajo y facilitando posibilidades (LEACH, 2014).

El Genio del Diseño Generativo: Algoritmos que Imaginan

El Diseño Generativo (DG) se define como un enfoque de diseño que utiliza algoritmos para generar proyectos (CAETANO et al., 2020). DG es un ciclo iterativo de aplicación y evaluación de reglas, lo que significa que el diseño inicial pasa por iteraciones mediante operaciones que involucran transformaciones geométricas y topológicas, evolucionando hacia el diseño resultante (BERNAL et al., 2015).

Algoritmos Evolutivos: Generadores de Soluciones Inspiradas en la Naturaleza

Los Algoritmos Evolutivos (AE) se originan de la ciencia computacional, específicamente en la inteligencia artificial, reproduciendo computacionalmente el proceso evolutivo de Darwin. Basados en cuatro pilares (población, diversidad, herencia y selección), su característica principal es la reproducción artificial de mecanismos evolutivos que permiten comportamientos adaptativos.

Similar a la naturaleza, este proceso se caracteriza por la integración e interacción entre un gran número de especies y sus variaciones, buscando el equilibrio con el entorno a través de la supervivencia del más apto. Este es el enfoque principal del uso de los AEs: buscar soluciones que resuelvan y satisfagan simultáneamente diferentes objetivos de un problema específico (FLOREANO y MATTIUSSI, 2008).

Muchos algoritmos simulan el funcionamiento de procesos naturales, los cuales, desde su descubrimiento por los humanos, no son concebidos y controlados por la mente humana, sino capturados, codificados y ejecutados por un sistema informático (TERZIDIS, 2006). Los AEs utilizan conceptos de mutación, selección y herencia, donde los individuos pueblan (población) un contexto específico, y los más aptos, basados en la teoría evolutiva, se determinan como el mejor resultado "fitness" (RUTTEN, 2013). Un AE consiste fundamentalmente en una población de soluciones codificadas (individuos) manipuladas por un conjunto de operadores y evaluadas por alguna función de aptitud (El uso de herramientas computacionales en oficinas de diseño es común desde mediados de los años 90 (VOLTOLINI, 2016). Estas herramientas de Diseño Asistido por Computadora (CAD) han optimizado significativamente la producción de proyectos, especialmente en términos de representación gráfica y visualización.

Los procesos de diseño son amplios y no universales, ya que cada individuo tiene procesos intrínsecos para expresar ideas. Sin embargo, se observan procesos comunes cuando se utilizan tecnologías específicas. Con las herramientas tradicionales (CAD), un proceso aditivo de inserción de información, la comprensión y generación resultan de la forma o composición espacial, conocido como FormMaking. En contraste, nuevas metodologías como el Diseño Paramétrico y la Modelación Algorítmica se inclinan más hacia FormFinding, un proceso que busca la forma basada en parámetros, ya sean fijos o manipulables (CARDOSO, 2017).

A través de métodos de Diseño Generativo (DG), los Algoritmos Evolutivos (AE) se han empleado en proyectos arquitectónicos, ayudando a dar forma tanto a la estructura de un edificio como a disposiciones geométricas que se alinean con factores ambientales. La idea fundamental es inspirarse en teorías evolutivas de la naturaleza para generar nuevas soluciones de manera más rápida.

Los algoritmos evolutivos se han utilizado para diseñar diversas tipologías de productos, desde aviones hasta chips de computadora, siendo adecuados para problemas donde la solución deseada no se conoce de antemano y el espacio de búsqueda es vasto y complejo.

En este enfoque de diseño, los algoritmos evolutivos simulan el proceso de selección natural, donde los miembros más aptos de una población se seleccionan para reproducirse y pasar sus características a la siguiente generación, generando múltiples soluciones (poblaciones). El algoritmo comienza con una población de diseños aleatorios, evaluando cada uno contra el objetivo deseado. Las soluciones se evalúan en relación con un conjunto de criterios llamados funciones de aptitud (ROHRMANN, 2019).

Los diseños más aptos se eligen para la reproducción, y sus características se combinan para crear nuevos diseños. Las soluciones que demuestran buen rendimiento según las funciones de aptitud se seleccionan para formar una nueva generación de soluciones. Este proceso se repite hasta alcanzar el objetivo deseado o la mejor opción dentro de un proceso finito (VOLTOLINI, 2020). La principal ventaja de este enfoque es su capacidad para encontrar excelentes soluciones para problemas difíciles de resolver para los humanos.

La historia de los algoritmos evolutivos. Nuevo paradigma de diseño

La historia de la programación de algoritmos evolutivos comienza con la idea de usar la evolución como metáfora para resolver problemas. Darwin, en su libro "El Origen de las Especies," propuso que los organismos evolucionan mediante un proceso de selección natural, donde los individuos más aptos tienen más probabilidades de sobrevivir y reproducirse. Esta lógica puede aplicarse a la resolución de problemas usando una población de soluciones potenciales, seleccionando las más aptas. Los primeros trabajos relacionados con la computación evolutiva se publicaron a mediados de los años 50 (JONG et al., 1997). Destacan los trabajos de Friedberg (1958), Friedberg et al. (1959) y Fraser (1957). En el mismo periodo, precisamente en 1962, Bremermann presentó sus primeros intentos de aplicar la simulación evolutiva y la optimización numérica para resolver problemas, desarrollando algunas de las primeras teorías sobre Algoritmos Evolutivos (JONG et al., 1997).

A mediados de los años 60, se establecieron las tres formas principales de Algoritmos Evolutivos (AE): la Programación Evolutiva (EP) por Lawrence Fogel en San Diego, California; los Algoritmos Genéticos (GA) por Holland de la Universidad de Michigan; y las Estrategias Evolutivas (ES) desarrolladas por un grupo de estudiantes en Berlín: Nienert, Rechenberg y Schwefel (JONG et al., 1997). Estas tres técnicas de algoritmos evolutivos se conocen colectivamente como Algoritmos Evolutivos (AEs) (COELLO et al., 2007).

En los años 90, tuvo lugar el International Workshop on Parallel Problem Solving from Nature en Dortmund, fomentando la interacción entre diversas comunidades de investigación de algoritmos evolutivos. La interacción constante y creciente llevó a la terminología conocida como Computación Evolutiva, aún utilizada hoy en día (SCHWEFEL y MÄNNER, 1991). Los Algoritmos Evolutivos se han empleado para diseñar y optimizar una amplia gama de productos en diferentes sectores, incluidos proyectos arquitectónicos. En las últimas décadas, una de las áreas principales de exploración en arquitectura es el uso de herramientas computacionales aplicadas al proceso de diseño (KESTELIER y PETERS, 2006).

Algunas definiciones clave

Para una mejor comprensión, presentaremos definiciones de conceptos relacionados con los Algoritmos Evolutivos, como Algoritmo, Modelación Algorítmica, Programación Visual, Diseño Paramétrico, Modelo Paramétrico y Diseño Generativo.

Algoritmos, los pilares del diseño innovador

En su reconocido libro "Algorithmic Architecture," Terzidis define un Algoritmo como (TERZIDIS, 2013): "Un algoritmo es un procedimiento computacional para resolver un problema en un número finito de pasos. Involucra deducción, inducción, abstracción, generalización y lógica estructurada. Es la extracción sistemática de principios lógicos y el desarrollo de un plan de solución genérico" (TERZIDIS, 2006, p. 159).

Modelación algorítmica, más allá de los límites tradicionales

Se refiere específicamente al uso de lenguajes de script que permiten a los diseñadores ir más allá de las limitaciones de las interfaces de software de diseño convencional, ampliando la capacidad de modelar mediante la manipulación directa no de la forma sino del código. La modelación algorítmica generalmente puede realizarse utilizando lenguajes de programación de computadoras como RhinoScript. Sin embargo, con la dificultad de la programación, aplicaciones como Generative Components y Grasshopper permiten el uso de código con formas pictóricas (componentes) para la automatización (LEACH, 2014).

Programación Visual: creando el futuro del diseño con arrastrar y soltar

La programación visual permite la creación de algoritmos mediante la manipulación de componentes gráficos como íconos, botones y símbolos. Es posible realizar modelación paramétrica con características de programación visual sin necesidad de escribir una línea de código de texto. A diferencia del código tradicional donde se escriben líneas de texto en un compilador, la programación visual utiliza programas que contienen una interfaz donde se introducen componentes para formar el código que realizará la tarea. Un ejemplo de tal programa es Grasshopper, un complemento para Rhinoceros (CELANI y VAZ, 2012).

Diseño Paramétrico: un cambio radical en la evolución dinámica de proyectos

El software paramétrico utiliza parámetros numéricos y geométricos, permitiendo ajustes incrementales a un elemento que consecuentemente afecta todo el modelo en una reacción en cadena. A diferencia del proceso tradicional, el diseño paramétrico interconecta partes del proyecto y las altera juntas, de manera integrada. Esta conexión permite cambios, relaciones, adiciones y reparaciones en el diseño, reduciendo el retrabajo y facilitando posibilidades (LEACH, 2014).

El genio del diseño generativo: algoritmos que imaginan

El Diseño Generativo (DG) se define como un enfoque de diseño que utiliza algoritmos para generar proyectos (CAETANO et al., 2020). DG es un ciclo iterativo de aplicación y evaluación de reglas, lo que significa que el diseño inicial pasa por iteraciones mediante operaciones que involucran transformaciones geométricas y topológicas, evolucionando hacia el diseño resultante (BERNAL et al., 2015).

Algoritmos evolutivos: generadores de soluciones inspiradas en la naturaleza

Los Algoritmos Evolutivos (AE) se originan de la ciencia computacional, específicamente en la inteligencia artificial, reproduciendo computacionalmente el proceso evolutivo de Darwin. Basados en cuatro pilares (población, diversidad, herencia y selección), su característica principal es la reproducción artificial de mecanismos evolutivos que permiten comportamientos adaptativos.

Similar a la naturaleza, este proceso se caracteriza por la integración e interacción entre un gran número de especies y sus variaciones, buscando el equilibrio con el entorno a través de la supervivencia del más apto. Este es el enfoque principal del uso de los AEs: buscar soluciones que resuelvan y satisfagan simultáneamente diferentes objetivos de un problema específico (FLOREANO y MATTIUSSI, 2008).

Muchos algoritmos simulan el funcionamiento de procesos naturales, los cuales, desde su descubrimiento por los humanos, no son concebidos ni controlados por la mente humana, sino que son capturados, codificados y ejecutados por un sistema informático (TERZIDIS, 2006). Los AE utilizan conceptos de mutación, selección y herencia, donde los individuos pueblan (población) un contexto específico, y los más aptos, basados en la teoría evolutiva, se determinan como el mejor resultado "aptitud" (RUTTEN, 2013). Un AE consiste fundamentalmente en una población de soluciones codificadas (individuos) manipuladas por un conjunto de operadores y evaluadas por alguna función de aptitud (COELLO et al., 2007).

Explorando el espectro de algoritmos evolutivos: de GA a ES

Existen varios tipos de algoritmos evolutivos, con tres técnicas principales aplicadas desde el concepto de AE conocidas como algoritmos genéticos, programación evolutiva y estrategias evolutivas.

Genetic Algorithms (GAs): imitando la evolución para mejores resultados de diseño

El primer algoritmo en utilizar esta idea fue el algoritmo genético (GA), propuesto por John Holland en la década de 1960. GA es un algoritmo de búsqueda que utiliza una población de soluciones potenciales y aplica operadores como selección, cruce y mutación para producir nuevas generaciones de soluciones (JONG et al., 1997).

Evolutionary Programming (EP): adaptando la inteligencia al diseño

Idealizada por Lawrence J. Fogel en 1960 mientras era asistente especial en la Fundación Nacional de Ciencias (NSF), EP consideraba que, en ese momento, la inteligencia artificial se concentraba en heurísticas y la simulación de redes neuronales primitivas, enfoques limitados ya que modelan a los humanos y no el proceso de producción de individuos, relacionándolo con el proceso evolutivo. Así, entendió que la inteligencia debía basarse en adaptar el comportamiento a una variedad de entornos (JONG et al., 1997). En EP, un individuo en una población está representado por una máquina de estados finitos (FSM), y la reproducción de la población y la generación de descendientes de todos los individuos se realizan mediante operadores de mutación. En la selección de individuos para la siguiente generación, los descendientes compiten con los padres, y solo los individuos con mayor aptitud, tanto de la generación actual como de los descendientes, sobreviven (GABRIEL, 2013).

Evolution Strategies (ES): optimizando el diseño con precisión biológica

La primera versión de las estrategias evolutivas (ES) apareció en 1964, llevada a cabo por estudiantes de la Universidad Técnica de Berlín: Bienert, Rechenberg y Schwefel, durante estudios de tecnología aeroespacial. Después de intentos fallidos utilizando estrategias manuales, Rechenberg imaginó usar datos para decisiones aleatorias, ejecutadas con éxito más tarde por Schwefel en una calculadora mecánica y por Bienert (1967) en la creación de un robot que realizaba acciones y decisiones automáticamente (JONG et al., 1997).

Referencias:

BERNAL, Marcelo; HAYMAKER, John R.; EASTMAN, Charles. On the role of computational support for designers in action. Design Studies, [s. l.], v. 41, ed. Part B, p. 163-182, 2015.

CAETANO, Inês; SANTOS, Luís; LEITÃO, António. Computational design in architecture: Defining parametric, generative, and algorithmic design. Frontier of Architectural Research, [s. l.], v. 9, p. 287-300, 2020.

CARDOSO, Carmo Gonçalves Machado. Performance-based Design: From form making to form finding. 2017. Tese (Mestrado) - Instituto Técnico de Lisboa, [S. l.], 2017.

CELANI, G.; VAZ, C. E. V. Scripts em CAD e ambientes de programação visual para modelagem paramétrica: uma comparação do ponto de vista pedagógico. In: Cadernos Proarq. Revista do Programa de Pós-graduação em Arquitetura da UFRJ, Rio de Janeiro: v.1, n. 18, p. 177-194, 2012.

COELLO, Carlos A. Coello; LAMONT, Gary B.; VELDHUIZEN, David A. Van. Evolutionary Algorithms for Solving Multi-objective Problems. Springer, [s. l.], ed. Second Edition, 2007.

FLOREANO, Dario; MATTIUSSI, Claudio. Bio-Inspired Artificial Intelligence: Theories, Methods, and Technologies. Cambridge, Massachusetts London, England: The MIT Press, 2008.

FRASER, A.S. Simulation of Genetic Systems by Automatic Digital Computers. Australian Journal of Biological Sciences, vol 10, p 484-491, 1957.

FRIEDBERG, Richard M. A Learning Machine: Part I. IBM Journal of Research and Development, vol. 2, no. 1, p. 2-13, 1958.

FRIEDBERG, Richard M.; DUNHAM, Bradford; NORTH, J. H. A Learning Machine: Part II. IBM Journal of Research and Development, vol. 3, no. 3, p. 282-287, 1959.

GABRIEL, Paulo Henrique Ribeiro; DELBEM, Alexandre Cláudio Botazzo. Fundamentos de algoritmos evolutivos. [S.l: s.n.], 2008.

JONG, Kenneth De; FOGEL, David B.; SCHWEFEL, Hans-Paul. A history of evolutionary computation. In book: Handbook of Evolutionary Computation, Oxford University Press, p. A2.3:1-A2.3:12, 1997.

LEACH, Neil. Parametrics Explained. Next Generation Building, [s. l.], v. I, 2014.

MAKKI, M., SHOWKATBAKHSH, M. and SONG, Y. (2019) ‘Wallacei Primer 2.0’, [Online].

Available at wallacei.com

KESTELIER, Xavier de; PETERS, Brady. Computation Works: The Building of Algorithmic. Architectural Design, [s. l.], v. 83, ed. 2, p. 8-15, 2013.

ROHRMANN, Jacqueline. Design Optimization in Early Project Stages: A Generative Design Approach to Project Development. 2019. Dissertação (Mestrado em Engenharia Civil) - Technical University of Munich, Munich, 2019.

RUTTEN, David. Galapagos: On the Logic and Limitations of Generic Solvers. Architectural Design, v.83, n. 2, p. 132-135, 2013.

SCHWEFEL, Hans-Paul; MÄNNER, Reinhard. Parallel Problem Solving from Nature: 1st Workshop, PPSN I Dortmund, FRG, October 1–3, 1990 Proceedings. Lecture Noter in Computer Science, [s. l.], v. 496, 1991.

TERZIDIS, Kostas. Algorithmic Architecture. [S. l.]: Architectural Press, p. 159, 2006.

VOLTOLINI, Giovani. Design Paramétrico e Modelagem Algorítmica: Os Efeitos De Seus Conceitos e Técnicas em Académicos de Arquitetura. 2016. Tese (Mestrado) - Universidade Federal de Santa Catarina, [S. l.], 2016.

VOLTOLINI, Giovani; PUPO, Regiane Trevisan; QUEIROZ, Natália. Design paramétrico e modelagem algorítmica: os efeitos de seus conceitos e técnicas para o estudante de arquitetura. Revista Geometria Gráfica, [s. l.], v. 4, ed. 1, p. 75-93, 2020.