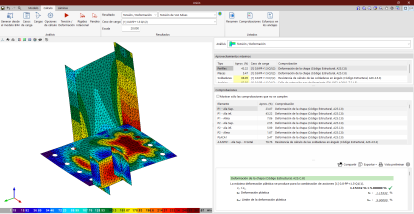
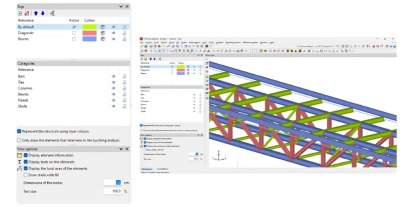
La soldadura es uno de las técnicas de unión que nos permiten ensamblar distintos elementos estructurales en acero.
Este artículo queda dividido en dos partes. La Parte I pretende ser una introducción a las tensiones en una soldadura. En la Parte II nos centraremos en la unión articulada entre viga y columna que se resolverá mediante soldadura a ambos lados del alma de la viga. Se trata de una unión muy sencilla que nos ayudará a identificar qué tensiones solicitan al cordón. En este artículo nos basaremos en la normativa española del Código Técnico de la Edificación en su Documento Básico de Acero estructural “CTE DB-SE-A”.
Próximamente en otro artículo resolveremos el mismo problema con normativa americana AISC-360.
PLANOS DE TRABAJO EN EL CORDÓN DE SOLDADURA

Figura 1 Geometría y planos del cordón de soldadura en ángulo
Figura 1 Geometría y planos del cordón de soldadura en ángulo
Los cordones de soldadura en ángulo dispuestos a ambos lados del alma de la viga se asimilan a un triángulo configurando la sección aproximada del cordón.
Distinguimos entre dos tipos de planos resistentes dentro del cordón:
Planos abatidos: son los dos planos ortogonales que cierran el triángulo de la sección aproximada.
Plano de garganta: se considera que es el plano resistente de la soldadura y forma 45º respecto a los planos abatidos.
INTRODUCCIÓN A LAS TENSIONES SOBRE EL CORDÓN
Los esfuerzos que actúan sobre el cordón de soldadura deben transformarse a una tensión determinada. Recordemos que una tensión es la
relación de un esfuerzo entre un área resistente, por lo que en función del plano de trabajo del cordón con el que trabajemos, podemos hablar de las tensiones siguientes:
Tensiones en los planos abatidos: denominadas con letras alfanuméricas.
- “n” es la tensión normal de cálculo que actúa perpendicular al plano de una de las caras del cordón de soldadura.
-
 es la tensión tangencial de cálculo normal a la arista contenida en el plano de una de las caras de la soldadura.
es la tensión tangencial de cálculo normal a la arista contenida en el plano de una de las caras de la soldadura.
 es la tensión tangencial de cálculo paralela a la arista contenida en el plano de una de las caras de la soldadura.
es la tensión tangencial de cálculo paralela a la arista contenida en el plano de una de las caras de la soldadura.

Figura 2 Tensiones en el plano abatido del cordón
Tensiones en el plano de garganta: denominadas con letras griegas.
 es la tensión normal perpendicular al plano de la sección transversal del cordón; es paralela a la dirección del cordón.
es la tensión normal perpendicular al plano de la sección transversal del cordón; es paralela a la dirección del cordón.- es la tensión normal de cálculo que actúa en la sección de la garganta.
 es la tensión tangencial de cálculo normal a la arista referida al plano de garganta.
es la tensión tangencial de cálculo normal a la arista referida al plano de garganta. es la tensión tangencial de cálculo paralela a la arista referida al plano de garganta.
es la tensión tangencial de cálculo paralela a la arista referida al plano de garganta.

Figura 3 Tensiones en el plano de garganta del cordón
CONVERSIÓN DE TENSIONES
Es habitual identificar en primera instancia las
tensiones en los planos abatidos 
y, de acuerdo a la solicitación sobre la unión, transformar estas tensiones del plano abatido en
tensiones sobre el plano de garganta 
Para ello podemos hacer uso de las siguientes expresiones:

A continuación veremos un ejemplo práctico de unión viga-columna articulada:

Figura 4 Geometría de la unión
Y nos apoyaremos en una
hoja de cálculo MathCad bajo los condicionantes de la norma española de estructuras en acero “
CTE DB-SE-A”.

Figura 5 Previsualización hojas de cálculo
¿Interesante? Puedes consultar este ejemplo y descargar la hoja de cálculo sobre la unión articulada

PARTE II
EJEMPLO PRÁCTICO según CTE “Código Técnico de la Edificación”
Geometría de la unión:

Figura 6 Geometría de la unión
DATOS DE PARTIDA
- Columna: HEB 200. - Garganta “a”: 5 mm.
- Viga: IPE 360. - L: 165 mm.
- Solicitación:
V= 250 kN (Esfuerzo cortante mayorado).
Para desarrollar este ejemplo, te invitamos a descargarte la siguiente hoja de cálculo:
descargar la hoja de cálculo sobre la unión articulada
En este caso el esfuerzo cortante actúa en la misma dirección que el plano abatido, paralelamente a la arista del cordón. Por este motivo tendremos
únicamente tensión tangencial en el plano abatido 
Esta tensión será absorbida por el plano de garganta


Recordemos que disponemos
dos cordones de soldadura a lado y lado del alma de la viga, de ahí el factor 2 en el denominador de la expresión anterior. Reemplazando valores se obtiene una tensión en el plano de garganta de:

Figura 7 Tensiones en el plano abatido y plano de garganta
Para validar el diseño de los cordones de soldadura debe cumplirse que la
Solicitación sea inferior a la
Resistencia del cordón como es obvio.
Obtenemos la tensión en el plano de garganta de acuerdo a la expresión de
Von Mises:

Figura 8 Tensión de comparación-solicitación de Von Mises
Seguidamente buscamos la resistencia del cordón de acuerdo a la expresión 8.23 del DB-SE-A. Fijémonos como esta resistencia del cordón es función de la
tensión de rotura de las chapas a unir “f
u” y de dos
coeficientes parciales de seguridad 

Ya por último buscamos el
porcentaje de aprovechamiento de la soldadura que es la relación entre la Solicitación y la Resistencia del cordón. Debe verificarse que el aprovechamiento sea inferior al 100%.

Finalmente lo que hacemos es verificar el cumplimiento de
dos limitaciones geométricas que hacen referencia a la garganta “a” del cordón en función del menor espesor de las chapas a unir “t
mín” por un lado, y por otro a la longitud “L” del cordón:

En este caso vemos como con los datos de partida considerados (a=5mm y L=165 mm) las soldaduras cumplen con todos los requisitos de dimensionado. El porcentaje de aprovechamiento del cordón está entorno al
70% y se considera válido. En cuanto a la longitud de los cordones de soldadura, en uniones articuladas se recomienda que sean inferiores a
2/3 del canto de la viga. Como es habitual se han dispuesto exactamente en una longitud de
1/2 del canto de la viga (330 / 2 = 165 mm).

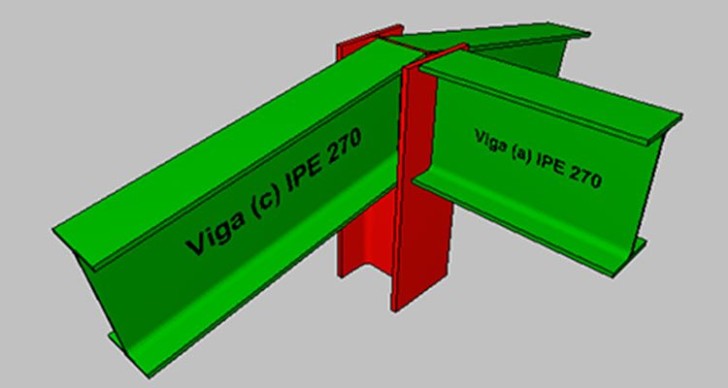



 A continuación veremos un ejemplo práctico de unión viga-columna articulada:
A continuación veremos un ejemplo práctico de unión viga-columna articulada:




 Recordemos que disponemos dos cordones de soldadura a lado y lado del alma de la viga, de ahí el factor 2 en el denominador de la expresión anterior. Reemplazando valores se obtiene una tensión en el plano de garganta de:
Recordemos que disponemos dos cordones de soldadura a lado y lado del alma de la viga, de ahí el factor 2 en el denominador de la expresión anterior. Reemplazando valores se obtiene una tensión en el plano de garganta de:


 Ya por último buscamos el porcentaje de aprovechamiento de la soldadura que es la relación entre la Solicitación y la Resistencia del cordón. Debe verificarse que el aprovechamiento sea inferior al 100%.
Ya por último buscamos el porcentaje de aprovechamiento de la soldadura que es la relación entre la Solicitación y la Resistencia del cordón. Debe verificarse que el aprovechamiento sea inferior al 100%.
 Finalmente lo que hacemos es verificar el cumplimiento de dos limitaciones geométricas que hacen referencia a la garganta “a” del cordón en función del menor espesor de las chapas a unir “tmín” por un lado, y por otro a la longitud “L” del cordón:
Finalmente lo que hacemos es verificar el cumplimiento de dos limitaciones geométricas que hacen referencia a la garganta “a” del cordón en función del menor espesor de las chapas a unir “tmín” por un lado, y por otro a la longitud “L” del cordón:
 En este caso vemos como con los datos de partida considerados (a=5mm y L=165 mm) las soldaduras cumplen con todos los requisitos de dimensionado. El porcentaje de aprovechamiento del cordón está entorno al 70% y se considera válido. En cuanto a la longitud de los cordones de soldadura, en uniones articuladas se recomienda que sean inferiores a 2/3 del canto de la viga. Como es habitual se han dispuesto exactamente en una longitud de 1/2 del canto de la viga (330 / 2 = 165 mm).
En este caso vemos como con los datos de partida considerados (a=5mm y L=165 mm) las soldaduras cumplen con todos los requisitos de dimensionado. El porcentaje de aprovechamiento del cordón está entorno al 70% y se considera válido. En cuanto a la longitud de los cordones de soldadura, en uniones articuladas se recomienda que sean inferiores a 2/3 del canto de la viga. Como es habitual se han dispuesto exactamente en una longitud de 1/2 del canto de la viga (330 / 2 = 165 mm).