Estado límite de vuelco en zapatas

A  partir de cálculos y ejemplos, José Carlos Coya Piñeiro, codirector del Máster Internacional de Estructuras de Edificación con Cype nos explica cómo verificar los estados límites de las zapatas asociados al colapso total o parcial del terreno o con el fallo estructural de la cimentación.

Las zapatas deben verificar una serie de estados límite últimos, asociados con el colapso total o parcial del terreno o con el fallo estructural de la cimentación. Se trata de una cuestión técnica, independiente de la normativa, pero por poner el ejemplo del DB-SE-C serían:

 a) hundimiento 

b) deslizamiento 

c) vuelco 

d) estabilidad global 

e) capacidad estructural del cimiento 

En esta ocasión nos centramos en la verificación de vuelco. No suele ser relevante en edificios, pero puede ser crítica en muros de contención y en estructuras en ménsula como carteles, es decir, cuando existen importantes momentos sobre una zapata con pequeña carga vertical. 

El esquema básico de cálculo de la zapata a vuelco consiste en suponer que la zapata gira respecto a su arista.

Cálculo

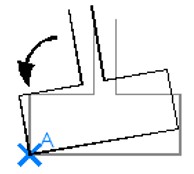
Para la comprobación a vuelco se determina un momento desestabilizador Mdesest -el que provoca el vuelco, debido a las acciones exteriores- y un momento estabilizador Mest , que generalmente solo se puede conseguir con la carga vertical permanente, transmitida por la estructura y el peso de la zapata. En ocasiones, también podemos contar con el peso del terreno o algún otro elemento que descanse sobre la zapata. 

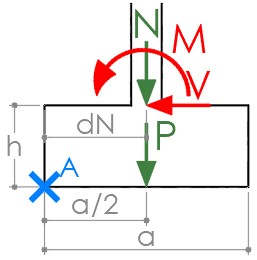
 El momento desestabilizador Mdesest es la suma del momento M transmitido por la estructura y el momento V·h generado por la fuerza cortante transmitido por la estructura multiplicada por el canto de la zapata. M desest=M + V·h El momento estabilizador Mest es la suma de los momentos generados por la carga vertical transmitida por la estructura (N·dN), por el peso de la zapata (P·a/2) y, en su caso, el momento generado por cualquier otra carga que actúe sobre la zapata. M est =N·dN+P·a/2 Si el pilar está centrado, dN=a/2 y por lo tanto M est=(N+P)·a/2 Existen diferentes maneras de aplicar la seguridad. Una manera muy interesante, porque da idea del margen de seguridad de la estructura, es obtener el coeficiente de seguridad de la estructura como  

Este es el método utilizado, por ejemplo, en la Guía de cimentaciones en obras de carretera, que exige que Fv sea mayor que 2 para combinaciones casi permanentes, mayor que 1.8 para situaciones características y 1.5 para combinaciones accidentales. El DB-SE-C usa un formato de seguridad diferente, que consiste en verificar que  

Donde γE es el coeficiente estabilizador de seguridad obtenido de la Tabla 2.1 del DB-SE-C. E En situaciones persistentes o transitorias, este coeficiente vale 1.8 para acciones desestabilizadoras y 0.9 para acciones estabilizadoras, que resulta equivalente a aplicar un coeficiente global 2

En situaciones extraordinarias este coeficiente vale 1.2 para acciones desestabilizadoras y 0.9 para acciones estabilizadoras, que resulta equivalente a aplicar un coeficiente global 1.33.

Ejemplo 1. Zapata de un cartel

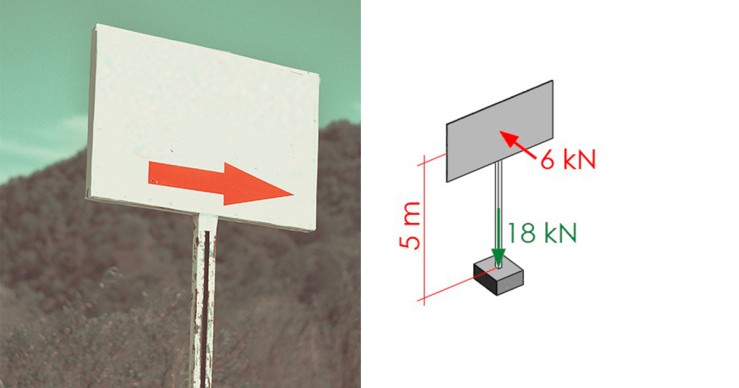
Supongamos un cartel de 2x3 m situado a 5 m de altura, con una carga de viento de 1 kN/m² y un peso total de 18 kN.

La resultante de la carga de viento da un total de 6 kN, que será el cortante en la base del soporte. Al estar situada a 5 m de altura, provoca un momento 6×5= 30 m·kN. 

Por lo tanto, las cargas exteriores de la zapata son las siguientes.

 Calculamos con una zapata de 2.00 m de lado y 0.50 m de canto.  

Los esfuerzos desestabilizadores son aquellos que provocan el vuelco en la zapata, en este caso el momento flector y el esfuerzo cortante.

Mdesest=M+V⋅h=30+60,50=30+3=33 m·kN

Los esfuerzos estabilizadores son aquellos que evitan el vuelco de la zapata, o sea, el esfuerzo axil y el peso propio del cimiento, que es 2,50×2,50×0,50×24.53=49.05 kN.

Mest=N·dN+P·a2=N+P·a/2=(18+49.05)2,00/2=67.05 m·kN

La comprobación a vuelco debe ser tal que:  

Donde: γE coeficiente parcial de seguridad que, según la Tabla 2.1 del DB-SE-C, presenta un valor de 0,9 para las acciones estabilizadoras y 1,8 para las acciones desestabilizadoras. Por lo tanto  

Ésta expresión es equivalente a  

Lo que significa que el dimensionado cumple esta verificación. Lo resumimos en una hoja de cálculo

Ejemplo 2. Zapata de un edificio

Comprobamos a vuelco una zapata de este edificio. Como ejemplo, analizamos el vuelco en dirección X en dos combinaciones:

• COMB1: Cargas permanentes y viento -Xesc-
• COMB2: Cargas permanentes, sobrecargas y viento -Xesc-

Las cargas en la base del pilar en estas combinaciones  

Podemos ver que cumple holgadamente en la combinación de cargas permanentes y viento. También vemos que si incluimos la sobrecarga, aunque el momento es algo mayor, el factor de seguridad aumenta porque aumenta aún más la carga vertical.

Coeficientes de seguridad de la estructura

Cuando calculamos la estructura de un edificio, que puede tener cualquier forma, el programa no sabe distinguir entre acciones estabilizadoras y desestabilizadoras en origen. Es decir, en cada combinación sabe si el axil, el cortante o el momento son estabilizadores o desestabilizadores, pero no lo sabe de las acciones que actúan sobre la estructura. En consecuencia, lo que hace es comprobar el vuelco para las combinaciones de acciones ELU de concreto/hormigón. Estas combinaciones son las de concreto/hormigón, del tipo 1.20·D+1.60·L si usamos ASCE/ACI, 1.35·G+1.50·Q si usamos CTE/CE. Por lo tanto, en el caso de tener zapatas que pueden estar comprometidas por vuelco es recomendable revisar la comprobación de vuelco manualmente, independientemente del cálculo que haga el programa.

Punto de giro

El cálculo habitual toma como eje de giro la arista de la zapata. La Guía de cimentaciones en obras de carretera propone un retranqueo de dicho eje de giro. 

No obstante, si se retranquea el eje de giro los coeficientes de seguridad exigidos son menores que si se sitúa en la arista.

Empuje pasivo del terreno

En el cálculo de vuelco no debe tenerse en cuenta la colaboración del empuje pasivo, a menos que pueda garantizarse que el terreno que lo produce esté siempre allí y tenga suficiente rigidez.

No obstante, con zapatas de poco canto el empuje pasivo no aportaría mucho a efectos de vuelco, porque el brazo mecánico es muy escaso. No obstante, cuando el canto es importante podría llegar a ser significativo.  

Esto conduce a otros métodos de cálculo, típico de farolas, postes de electricidad o comunicaciones y elementos similares. El clásico es el método de Sulzberger, que dejaremos para otra ocasión.