Blog / BIM & Construction Management
Categorias
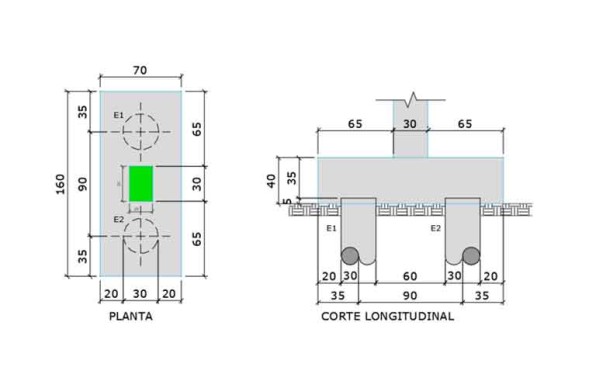
A geometria dos blocos de coroamento sobre estacas permite classificar os mesmos em dois tipos: rígidos ou flexíveis. Tal classificação determina como será feito o dimensionamento das armaduras do bloco. Este trabalho discute os critérios para a classificação da rigidez dos blocos e demonstrar na prática, através da análise de dois blocos de coroamento, e como classificar corretamente os mesmos.
Os blocos de coroamento sobre estacas são elementos de concreto que têm como propósito transferir os esforços dos pilares para as estacas. No entanto, estes elementos, em função da sua geometria, são classificados em 2 tipos: rígidos e flexíveis. Cada uma das classificações acima tem um comportamento estrutural distinto. Com o fim de trabalhar como elementos de rigidez, os blocos rígidos, não se deformam com a atuação da carga vertical dos pilares, transferindo a mesma de forma igual entre as estacas, desde que estas sejam equidistantes do pilar. Já os blocos flexíveis trabalham como elementos com menor rigidez, ou seja, que se deformam com a atuação da carga vertical dos pilares, transferindo-as de forma desigual para as estacas. Essa distribuição de cargas varia em função da distância do ponto de aplicação da carga concentrada do pilar. As estacas mais próximas aos pilares apresentam reações maiores do que as estacas que estão mais afastadas dos pilares.
É amplamente difundido no meio técnico que blocos rígidos com até 6 estacas devem ter seu dimensionamento estrutural realizado através de Métodos de Bielas e Tirantes e que blocos rígidos com mais de 6 estacas podem ter seu dimensionamento estrutural realizado conforme dita o Apêndice 4 do Information Bulletin 73, do CEB-70, ou mesmo através de Métodos de Bielas e Tirantes. Em função da complexidade da elaboração de um Modelo de Bielas e Tirantes, o mais comum, para blocos rígidos com mais de 6 estacas, é o dimensionamento estrutural realizado conforme dita o CEB-70. Já o dimensionamento estrutural dos blocos flexíveis, independentemente do número de estacas, deve ser feito considerando o bloco uma laje, respeitando os limites normativos para sua resistência ao cisalhamento, em função da inexistência de armadura resistente à este esforço. Logo, a correta classificação do bloco em função de sua rigidez é vital para o desempenho do elemento estrutural, visto que o comportamento estrutural do elemento é diferente para cada classificação. Um dos principais objetivos de um bom projeto estrutural é a economia, que deve sempre andar de mãos dadas com a segurança. Assim, é de boa prática buscar sempre as menores dimensões para os blocos de coroamento. Idealizar um bloco como rígido e dimensioná-lo, sendo ele, na verdade, um bloco flexível, pode levar à ruína uma estrutura, causando enormes prejuízos econômicos, desacreditando a boa engenharia e, principalmente, ceifando vidas humanas.
Para que um bloco seja rígido e, portanto, possa ser dimensionado por modelos de Bielas e Tirantes, existe um ângulo mínimo, medido entre a biela e o tirante, a ser atendido. Este valor é determinado, por vezes numericamente e por vezes pela razão de determinadas relações dimensionais, que nos levam à ângulos numericamente determinados. O ACI 318/2014 dita, em seu item 23.2.7, que “O ângulo entre o eixo de qualquer biela e qualquer tirante que atravesse um nó único deve ser de, no mínimo, 25 graus” (na tradução livre). Desta forma, simples e diretamente ele menciona o ângulo entre a biela e o tirante. Diante disso, a NBR 6118/2014, desde a sua versão de 2003 diz que a classificação dos blocos deve ser feita de forma análoga à das sapatas. O item 22.6 da NBR 6118/2014 diz que, para que as sapatas sejam consideradas rígidas, elas devem atender à relação: 
onde, h é a altura total da sapata; a é a extensão da sapata na direção considerada; ap é a dimensão do pilar na direção considerada;
Para compreender de onde vem tal classificação, precisamos olhar para o Apêndice 4 do Information Bulletin 73, do CEB-70. Este documento, é a base para a classificação e dimensionamento à flexão de elementos de transmissão de cargas para as fundações.
O CEB-70 indica que, para que uma sapata seja considerada rígida, ela deve atender aos seguintes critérios:
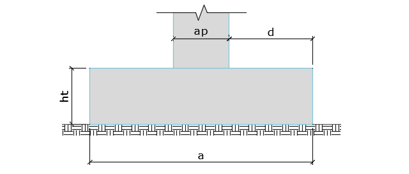Figura 1.a – Lajes apoiadas sobre o solo (CEB-70). 
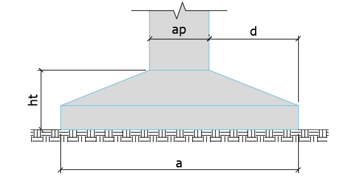Figura 1.b – Lajes apoiadas sobre o solo (CEB-70). 
Onde,
d é a distância entre a face do pilar e a extremidade da sapata; ht é a altura total da sapata; a é a extensão da sapata na direção considerada; ap é a dimensão do pilar na direção considerada;
Então,
Da Eq. 2, depreende-se que a altura da sapata, para que a mesma seja considerada rígida, deve ser tal que permita uma inclinação de 1:2, ou seja, um ângulo α de 26,56º.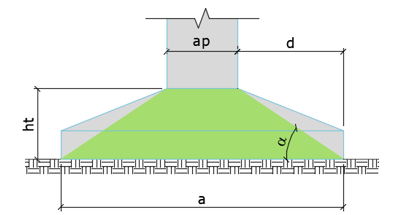 
Figura 2 – Ângulo verificado nas sapatas (CEB-70). Já para blocos, o CEB-70 indica que, para que o mesmo seja considerado rígido, ele deve atender ao seguinte critério: 
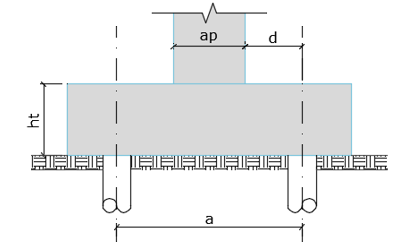Figura 3 – Lajes apoiadas sobre estacas (CEB-70).
Onde,
d é a distância entre a face do pilar e o centro das estacas mais afastadas; ht é a distância entre o topo da estaca e o topo do bloco; a é a distância entre as estacas mais afastadas na direção considerada; ap é a dimensão do pilar na direção considerada;
Fazendo as mesmas considerações feitas nas equações acima, encontramos:
Da Eq. 6, depreende-se que a altura do bloco, para que o mesmo seja considerado rígido, deve ser tal que permita uma inclinação de 1:1,5, ou seja, um ângulo de 33,69º. Este é o valor mínimo do ângulo da biela mais afastada, previsto pela NBR 6118/2014, para classificar um bloco como rígido.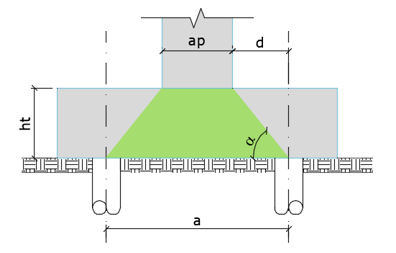 
Figura 4 – Ângulo a ser verificado nos blocos (CEB-70). Nesse sentido, alguns podem considerar que, para os blocos, o valor de ht deveria ser a altura total do bloco, assim como o é nas sapatas. Entretanto, é simples compreender que este valor deve ser considerado à partir do topo da estaca. Na figura original do CEB-70, Figura 3 deste artigo, observa-se que a estaca termina imediatamente abaixo do fundo do bloco. Não foi considerado nesta figura o embutimento da estaca. Portanto, a inclinação a ser verificada, pelo texto original do CEB-70, é a indicada na figura 4. Portanto, a altura que deve ser considerada para a determinação da inclinação do bloco é a altura útil, caracterizada por: 
Onde,
d util é a altura útil; ht é a altura total da bloco; emb é a altura do embutimento da estaca dentro do bloco; y c.g. é a distância do topo da estaca ao centro de gravidade do feixe de armaduras, considerando a possibilidade de mais de uma camada de barras de aço;
Quanto maior o embutimento da estaca e maior o número de camadas de barras de aço, para um mesmo ht, menor será a altura útil e, consequentemente, a inclinação da biela. Também é preciso analisar o ponto de saída da biela, no pilar. Em sapatas, as cargas se distribuirão uniformemente à partir do perímetro do pilar, em direção ao perímetro da sapata (Figura 5).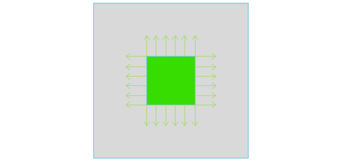 
Figura 5 – Cargas espraiando uniformemente. Isto valida o ponto de partida da inclinação da sapata a ser verificada na face do pilar, conforme mostra a Figura 2. Entretanto, nos blocos rígidos, as bielas partem de um ponto interno ao pilar. Para se determinar este ponto, divide-se o pilar em n quadrículas de áreas equivalentes, onde n é o número de estacas. As bielas partirão do centro de gravidade das quadrículas em direção ao centro de gravidade das estacas. Por exemplo, um bloco de 2 estacas terá o pilar dividido em 2 quadrículas. O centro de gravidade destas localizam-se à 1/4 da dimensão do pilar na direção considerada (Figura 6). Como outro exemplo, um bloco de 10 estacas terá o pilar dividido em 10 quadrículas e assim sucessivamente. Para um bloco de 2 estacas, o ângulo da biela ∝ será dado por: 
Desta forma, nota-se que a inclinação da biela deve ser verificada conforme indicada na Figura 6, o que nos dá bielas bem mais abatidas do que as verificadas quando tomados os pontos de partida originais do CEB-70.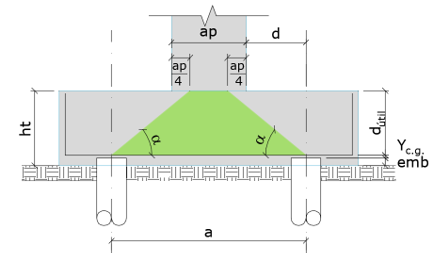 
Figura 6 – Ângulo a ser efetivamente verificado. A seguir será demonstrada uma metodologia adequada para a correta classificação dos blocos segundo sua rigidez através de 2 modelos: um com 2 estacas e um com 10 estacas.
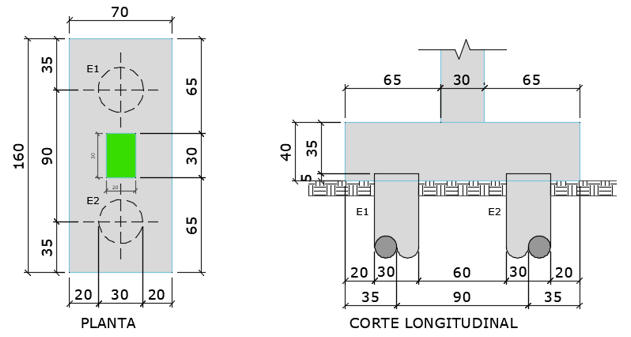Figura 7 – Geometria do bloco de 2 estacas. O primeiro passo é determinar a altura útil, conforme a Equação (8). Para tanto, é necessário arbitrar um diâmetro de barra para o tirante. Inicialmente, adotaremos uma bitola de 12,5mm. 
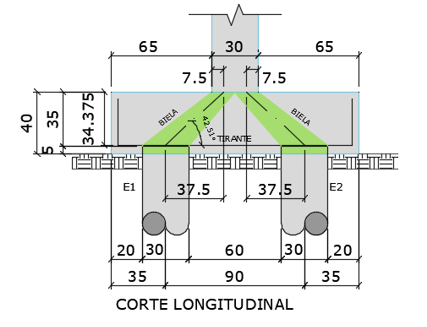Figura 8 – Ângulo efetivo da biela.
Da Equação (9) obtemos o ângulo da biela:
Como o valor de ∝ encontrado é maior do que o ângulo mínimo de 33,69º, este bloco é considerado rígido.
Para determinar a classificação do bloco da Figura 9, é preciso, primeiramente, subdividir o pilar nas suas respectivas quadrículas. O pilar terá, portanto, 10 quadrículas de igual área. Do centro de cada quadrícula (Q1,Q2,...,Q10) a biela partira em direção à sua respectiva estaca (E1, E2, ..., E10). Em segundo lugar, é preciso determinar a distância, no plano, entre o C.G. da estaca e o C.G. da quadrícula, como visto na Figura 10. Esta distância é dada por: 
Onde,
ex é a distância no sentido x= 320,0cm; ey é a distância no sentido y= 100,0cm;
Em terceiro lugar, é necessário determinar a altura útil, conforme a Equação (8). Adotaremos uma bitola de 20mm para esta verificação. 
Temos portanto que o ângulo da inclinação da biela mais afastada é dado por:
Como o valor de ∝ encontrado é menor do que o ângulo mínimo de 33,69º, este bloco é considerado flexível e não poderia, de forma alguma ser considerado como rígido, devendo seu dimensionamento obedecer os preceitos de dimensionamento de lajes.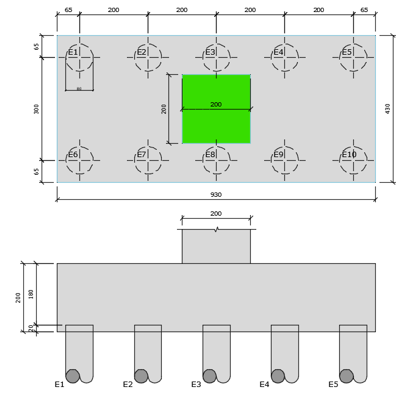 
Figura 9 – Geometria do bloco de 10 estacas. 
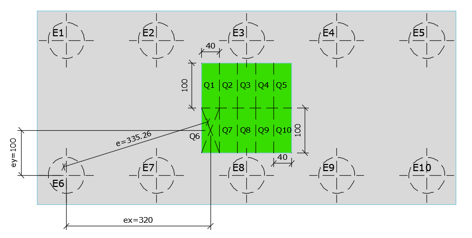Figura 10 – Determinação da distância entre os C.G.'s. Então, faz-se necessária a obtenção das reações das estacas através de um modelo de grelhas ou elementos finitos, visto que, em função da flexibilidade da laje, cada par de estacas terá uma reação distinta. Caso haja a atuação de momentos fletores, cada estaca terá uma reação distinta.
É imprescindível compreender que, para a correta classificação dos blocos em função da sua rigidez, o que deve ser verificada é a inclinação da biela de compressão da estaca mais afastada, em direção ao centro geométrico da respectiva quadrícula. O ACI 318/14 faz essa afirmação de forma objetiva, declarando que o que deve ser verificado é a biela. Caso seja feita a verificação apenas da relação entre a distância do eixo da estaca (no plano) até a face do pilar e a altura total do bloco, como dá a entender a NBR 6118/2014, logo, estará cometendo um equívoco conceitual. Por exemplo, considerando a Equação 1, presente na NBR 6118/2014, e utilizando a distância a=800cm (distância no plano entre os centros das estacas mais afastada) e a dimensão do pilar na direção considerada (ap=200cm), como dá a entender a Figura 3 extraída do CEB-70), a altura mínima necessária para o bloco seria de 200cm, conforme aplicação a seguir: 
Isto geraria um ângulo da biela de 33,69º, o que, equivocadamente, levaria o profissional a dimensionar como rígido um bloco que é, como devidamente mostrado no Modelo 2, flexível. Como o que deve ser verificado é, na realidade, a inclinação da biela, o concreto que fica abaixo dela, a altura de embutimento da estaca dentro do bloco, não contribui em nada para a rigidez do bloco. Esta análise invalida, por completo, a redação do item 22.7.1 da NBR 6118/2014. Sugere-se que este item tenha sua redação revisada, considerando os preceitos indicados neste trabalho.
AMERICAN CONCRETE INSTITUTE. ACI 318 – Building Code Requirements for Structural Concrete. 2014. COMITÉ EUROPEÉN DU BÉTON – Information Bulletin nº 73 – FIP - International Recommandations for the Design and Construction of Concrete Structures. Vol. 2: Appendixes - Proposals. ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS – NBR 6118 - Projeto de estruturas de concreto – Procedimento. 2014.
Márcio Roberto da Cunha e Everton Rodrigo de Moura
