Na década de 1960 os métodos matriciais eram a única escolha para os programas de análise estrutural e pesquisas subseqüentes, fizeram o método da rigidez como o mais eficiente a ser implementado em códigos computacionais do que os métodos tradicionais.
Infelizmente, esta eficiência computacional não contribuiu da forma esperada para o entendimento do aluno, especialmente quando alunos de graduação estão tentando entender os conceitos da análise estrutural.
A integração computacional nos cursos de engenharia tem sido objeto de estudo por parte de educadores há mais de trinta e cinco anos. Quando os programas computacionais são introduzidos nos cursos de análiseestrutural, a instrução é geralmente limitada ao seu uso e, conseqüentemente, alguns detalhes sobre a análise passam despercebidos, pois alguns destes programas funcionam como uma “caixa-preta”.
Atualmente têm-se disponíveis mais recursos computacionais do que há vinte anos. Além disto, vários progr mas têm sido desenvolvidos, tais como: Excel®, Matlab®, Maple®, entre outros, nos quais os alunos podem utilizar para modelar os métodos tradicionais da análise estrutural.
Planilhas eletrônicas
De acordo com ROCHESTER (1993) o desenvolvimento das planilhas eletrônicas deu-se início com Dan Bricklin, um estudante de mestrado em administração que pensou que deveria haver uma melhor forma de resolver os cálculos tediosos de seus estudos. Ele perguntou a um de seus amigos da área de informática, Bob Frankston, se ele poderia desenvolver um código computacional que pudesse resolver seus problemas. Em 1978 Frankston concordou e em janeiro de 1979 a primeira planilha eletrônica foi feita.
Esta planilha foi chamada de VisiCalc® e foi originalmente desenvolvida para aplicações em contabilidade e posteriormente os profissionais da engenharia, devido à formação matemática, encontraram inúmeras aplicações para a planilha eletrônica. Foi um impacto tão grande que empresas como a Microsoft® incorporaram várias funções de engenharia nas suas planilhas.
A planilha eletrônica é uma aplicação interativa e é dividida em várias células. Cada célula é independente e suas propriedades podem ser referenciadas em qualquer parte da planilha. Isto significa que a planilha pode ser construída para que as células trabalhem em conjunto ou de uma forma isolada.
Método de Cross
Na análise estrutural quanto maior é a complexidade da estrutura, maior é o número de incógnitas e, conseqüentemente, maior é o número de equações a serem resolvidas. Métodos
manuais de análise tornam-se extremamente tediosos quando a estrutura possui um elevado número de nós ou elementos. Uma alternativa óbvia é utilizar recursos computacionais para
resolver tais tipos de estrutura. Entretanto, pode-se utilizar também um procedimento iterativo conhecido como o Método da Distribuição dos Momentos.
O artigo do Professor CROSS (1930) da Universidade de Illinois nos Estados Unidos descreve o proce dimento completo para a análise de pórticos por distribuição dos momentos de engastamento, método hoje mundialmente conhecido como Método de Cross. O
Método de Cross é um processo iterativo de solução das equações de equilíbrio baseado no método da relaxação sem a obtenção explícita dos deslocamentos. O efeito dos esforços axiais não é considerado no método. Obtém-se, na conclusão do processo, os momentos fletores nas extremidades dos elementos que formam a estrutura.
O procedimento é iniciado assumindo todos os nós da estrutura temporariamente restringidos contra deslocamentos , ou seja, a estrutura é primeiramente tornada cinematicamente determinada, procedimento característico do método dos deslocamentos, e os momentos de engastamento dos elementos , causados pelo sistema de forças aplicado à estrutura, são determinados para esta condição. Em seguida, um nó de cada vez é liberado e, então, é realizada a distribuição dos momentos resultante s nas extremidades dos elementos conectados ao nó liberado, que por sua vez, geram momentos nos nós adjacentes que ainda se encontram restringidos, satisfazendo desta forma as condições de compatibilidade geométrica ou continuidade. O nó liberado é novamente restringido e um outro nó é solto com o processo sendo repetido quantas vezes forem necessárias até que os momentos gerados nos nós restringidos adjacentes sejam nulos ou de valor numericamente insignificante. Os momentos fletores finais em cada uma das extremidades dos elementos são obtidos pela somatória dos momentos calculados nestas extremidades.
A convenção de sinais é a de que os momentos fletores serão considerados positivos quando atuarem na extremidade do elemento no sentido horário, assim como, a rotação no nó no sentido horário será também considerado positivo.
Alguns par metros
Analisando uma estrutura pelo Método de Cross são empregados alguns parâmetros denominados de rigidez rotacional, rigidez rotacional reduzida, fator de distribuição e fator de transmissão, além dos momentos de engastamento que podem ser determinados por qualquer um dos métodos de análise estrutural encontrados na literatura.
No Método de Cross inicialmente todos os nós são restritos (engastados) e o processo de iteração é realizado, de forma geral, com apenas um nó liberado e os demais restringidos de
maneira que a análise da estrutura seja feita conforme a Figura 1.

Figura 1 – Estrutura apoiada em uma extremidade e engastada na outra.
Pode-se proceder de forma análoga para elementos com rótula nas extremidades. No entanto, sabendo-se que o momento fletor na rótula é igual a zero e que o processo de iteração é simplificado utilizando-se a rigidez rotacional reduzida para elementos com rótulas em suas extremidades. Fazendo-se o uso da rigidez rotacional reduzida quando o nó i adjacente à uma
estrutura rotulada j é liberado, tem-se a estrutura indicada na Figura 2.

Figura 2 – Estrutura bi-apoiada
Após a determinação dos momentos de engastamento nas extremidades dos elementos que constituem a estrutura, cada nó é liberado um de cada vez e conseqüentemente no instante em que um determinado nó é liberado, com os demais nós adjacentes restringidos, o momento resultante no nó liberado provocado pela soma algébrica dos momentos de engastamento existentes naquele nó é distribuído a cada extremidade do elemento pertencente ao nó liberado.
Essa distribuição do momento resultante no nó liberado, em cada iteração, é diretamente proporcional à rigidez rotacional das extremidades dos elementos conectados ao nó liberado
por um fator denominado de Fator de Distribuição (FD).
Considerando um pórtico submetido a um sistema de força qualquer sendo analisado pelo Método de Cross na etapa em que o nó B é liberado, os momentos de engastamento nas extremidades dos elementos conectados ao nó B causam a rotação do nó e a correspondente
linha elástica ilustrada na Figura 3.

Figura 3 – Rotação no nó B .
Exemplo numérico
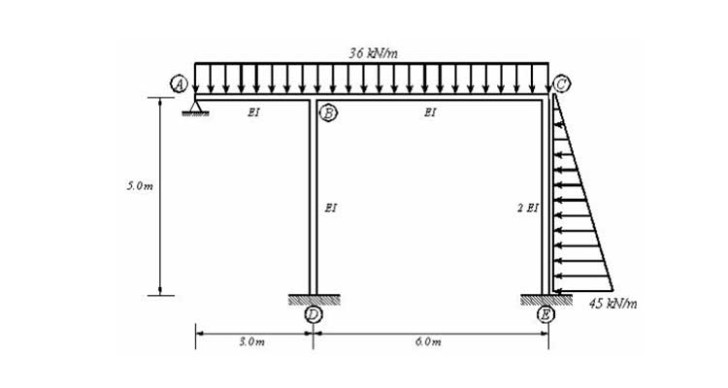
Para ilustrar a aplicabilidade do Excel® o exemplo consiste em um pórtico indeslocável dado por SILVA JR (1975). O apoio A é um apoio do segundo gênero e os apoios restantes são considerados como apoios do terceiro gênero. O carregamento e as características da estrutura são ilustrados na Figura 4 e a solução da estrutura, pelo Método de Cross, é presentada na planilha da Figura 5.

Figura 4 – Pórtico indeslocável.
A linha 4 da planilha da Figura 5 apresenta os fatores de distribuição que dependem do material e das propriedades geométricas da estrutura.
A linha 5 apresenta os momentos de engastamento nas extremidades e fazem parte da primeira iteração do método. É válido ressaltar que esses momentos dependem do tipo de carregamento que a estrutura está submetida. A linha 6 é obtida utilizando-se os momentos de engastamento nas extremidades, assim como, os fatores de distribuição. Por exemplo, a célula E6 é dada por = (D5 + E5 + F5) * (−1) * E4 . Observe que em cada iteração são utilizados os fatores de transmissão. Por exemplo, a célula J 9 é dada por = E8 * 0,5 . O procedimento para as demais iterações é feito de forma análoga. Deve-se ter atenção na utilização dos fatores de transmissão, pois no nó B existe a influência de três elementos: BA, BC e BD.
O resultado final dos momentos nas extremidades dos elementos é o somatório, nas respectivas colunas, das linhas 5 a 19. Por exemplo, o momento final da extremidade B do elemento BC , célula F21, é dado por = SOMA (F5 : F19) .

Figura 5 – Planilha do Excel® para o pórtico indeslocável.
A Figura 6 mostra o diagrama de momento fletor para pórtico da Figura 4 foi obtido utilizando-se o programa FTool®. Observe que os valores obtidos pelo programa estão de acordo com os obtidos pela planilha eletrônica.
No Método de Cross devem-se fazer várias iterações até que os momentos nas extremidades dos elementos sejam zero. No exemplo apresentados optou-se por fazer oito iterações para mostrar que na medida que se aumenta o número de iterações, o valor dos momentos tende a zero. Com a construção da planilha da Figura 5, pode-se facilmente alterar as propriedades geométricas da estrutura e o tipo de carregamento, alterando-se para tanto, as linhas 4 e 5, respectivamente.

Figura 6 – Diagrama de momento fletor para o pórtico indeslocável.
Considerações finais
Atualmente os alunos dos cursos de análise estrutural podem utilizar diversas ferramentas computacionais para realizarem os cálculos. As vantagens de se utilizar estas ferramentas em relação aos procedimentos manuais, incluem a redução de erros matemáticos, execução rápida de cálculos repetitivos e a exploração de configurações alternativas. A utilização de planilhas eletrônicas pode auxiliar o ensino do Método de Cross reduzindo o tempo gasto pelos alunos na resolução dos exercícios. Pode-se facilmente incluir nas planilhas apresentadas, carregamentos que envolvam efeito de temperatura, carga trapezoidal, carga concentrada e até mesmo molas e recalques de apoio. Acredita-se que os alunos, mesmo com conhecemos elementares de análise estrutural, possam resolver.
Arlindo P. Lopes – [email protected]
Li Chong Lee B. de Castro – [email protected]
Carlos Eduardo V. Neves – [email protected]